Accurate 3D Attenuation Map for SPECT Images Reconstruction
Hamida Romdhane1*, Mohamed Ali Cherni2 and Dorra Ben-Sellem1,3,4
1University of Tunis ElManar, ISTMT, LR13ES07 LRBTM, Tunis, Tunisia
2University of Tunis, ENSIT, LR13ES03 SIME, Moneury, 1008 Tunis, Tunisia
3University of Tunis ElManar, FMT, 1007 Tunis, Tunisia
4Department of Nuclear Medicine, Salah Azaiez Institute, 1006 Tunis, Tunisia
- *Corresponding Author:
- Hamida Romdhane
University of Tunis ElManar
ISTMT, LR13ES07 LRBTM, Tunis, Tunisia
Tel: +95544272
E-mail: romdhane.hamida@gmail.com
Citation: SRomdhane H, et al. Accurate 3D Attenuation Map for SPECT Images Reconstruction. Ann Med Health Sci Res. 2020;10: 832-837.
This is an open access article distributed under the terms of the Creative Commons Attribution?NonCommercial?ShareAlike 3.0 License, which allows others to remix, tweak, and build upon the work non?commercially, as long as the author is credited and the new creations are licensed under the identical terms.
Abstract
Background: Scintigraphic images are affected by the phenomenon of attenuation of gamma photons. To improve the quality of single photon emission computed tomography (SPECT) images, it is necessary to correct the attenuation. It is generally realized through the use of an attenuation map derived from Computed Tomography (CT). In this paper, we proposed a new 3-D map to correct the attenuation in SPECT images. The proposed method combines SPECT and CT medical imaging exams. XRay CT-images are used to extract lung regions, which will be multiplied by the lung’s Hounsfield Unit to finally obtain the 3D-attenuation map. This obtained map will be next used in SPECT image reconstruction by applying the 3-D maximum likelihood expectation maximization (MLEM) algorithm. Results show that the proposed method enhanced the quality of the SPECT images quantitatively and qualitatively. In fact, it increases the Image Quality Index, the structural similarity index and the peak of the signal to noise ratio of the obtained image comparing to other confirmed literature methods. In addition, it guarantees a lower value of the mean squared error. Otherwise, the superiority of the method is confirmed by the Dunnett” test t” which computes the significant difference of the obtained results. In fact, the proposed method obtained a p-value (inferior to 0.05) for all executed tests.
Keywords
Attenuation map; Attenuation correction; 3-D MLEM; Reconstruction; SPECT images
Introduction
Scintigraphic imaging is an emission imaging that is based on the administration of radio-pharmaceuticals. Radio-pharmaceutical is the chemical coupling between a cold molecule specific of organ and a radioactive isotope. In Single-photon emission computed tomography (SPECT), the radionuclide (99mTc in this work) is a low-energy gamma photon emitter (140 Kev). These photons by crossing the patient, to be detected by the gamma camera, will be attenuated, which alters the quality of the image (the lower the energy of the radionuclide, the more the alteration is important). Effects of attenuation on image quality are the loss of a large number of photons which conducts to a decrease in SNR, the poor quantification and heterogeneity of the image (secondary to an attenuation dependent on the depth of the anomaly), with the possibility of non-visualization of deep lesions that are not very functional. So, attenuation correction is a crucial step to improve SPECT images. This correction is currently provided by the hybrid SPECT/CT machines, which couples a gamma camera and a diagnostic scanner. The scanner provides an attenuation map and improves the spatial location of functional abnormalities. SPECT is an acquisition modality of scintigraphic imaging, a diagnostic procedure of nuclear medicine. In such modality, the gamma camera rotates around the patient and takes images of the distribution of radiopharmaceuticals from different angles. These images are called projections. The procedure of assembling projections to obtain slice imaging is called image reconstruction. Tomographic reconstruction aims to obtain axial, coronal and sagittal slices of an object from its projections. Many algorithms have been adopted to reconstruct 3-D SPECT images from 2-D acquired projections. These methods have been widely used in the reconstruction of SPECT images because of their computation speed and their simple implementation. Historically, all image reconstruction methods have sought to reduce the problem of 3-D image reconstruction to a 2-D problem by dividing 2-D projection data into a 1-D profile to produce cross-sectional images of the object. These algorithms are often called 2-D reconstruction algorithms. [1,2] Recently, due to the massive increase in processing speeds of modern computers and the availability of cheap high-capacity memory chips, a new generation of image reconstruction algorithms has appeared. These algorithms allowed the complete 3-D reconstruction of projection data. To accurately correct SPECT images from photon cross-talk between transaxial slices, a fully 3-D reconstruction is required. Contrary to 2D-reconstruction, slice by slice, the complete 3-D reconstruction uses a large matrix to take into account photons detected in the out-of-slice projection pixels. [3] In comparison to 2-D reconstruction, the accuracy and the signal-to-noise ratio (SNR) have been significantly improved. [4] In this paper, we propose a new 3-D attenuation map from patient Computed Tomography (CT) exams. The reconstruction is based on the analytic filtered back projection (FBP) algorithm. The organization of this paper is described as follow: section 2 describes the principle of acquisition of SPECT, cites the problem of attenuation in SPECT images and describes the proposed method. Section 3, exposes simulation results followed by an evaluation study proving the accuracy of the proposed method. Finally, we summarize the different steps of the proposed method and the evaluation results.
Methods
Scintigraphy is based on the administration of radioactive tracers (radio-pharmaceuticals) which binds to the target organ, emitting gamma rays. These rays will be detected by a gamma camera. SPECT is one of the modalities of this imagery where the gamma camera rotates around the patient to record several images of the radioactive concentration at different projection planes. For each angular position, a projection is acquired. These projections cannot be used in clinical exams. They should be reconstructed to be exploited and to allow doctors performing their diagnosis. Two types of algorithms are used in reconstructing images: an analytical algorithm or iterative algorithm.
Reconstruction algorithms
Analytical reconstruction algorithms: Filtered backprojection:
FBP is the most commonly used reconstruction algorithm in SPECT imaging. This is principally due to the simple concept of the algorithm and to the relatively quick processing time. FBP can be viewed as a two-step process: filtering of the data and back projection of the filtered projection data. There is extensive literature on these reconstruction algorithms and reviews of FBP and its applications to SPECT. [5,6]
Iterative reconstruction algorithms:
The general concept of iterative methods is to find a vector f that is a solution of g =A.f, [7] with g the vector of values in the sinogram, A a given matrix and f the unknown vector of pixel values in the image to be reconstructed. The principle of iterative algorithms is to find a solution through successive estimates. Measured projections are compared with projections corresponding to the current estimate. The aim of this comparison is to modify the current estimate, thus creating a new one.
Algorithms differ in the way estimated and measured projections are compared and the type of correction applied to the current estimate. The procedure is initiated by arbitrarily creating a first estimate. The used image is a uniform black or white image (depend on whether the correction is carried out under the form of an addition or a multiplication). [8]
Iterative reconstruction methods are classed in two categories: algebraic algorithms like Algebraic Reconstruction Technique (ART) and its accelerated version Simultaneous Algebraic Reconstruction Technique (SART) and statistical algorithms such as maximum likelihood expectation maximization (MLEM) and Ordered-Subsets Expectation Maximization (OSEM). [1] For SPECT reconstruction, iterative reconstruction algorithms have several advantages over analytical reconstruction algorithms, because many imaging physics, such as non-uniform attenuation and scatter, can be modeled in the matrix, [3] whereas they are difficult to handle in an analytic algorithm. [9] One of the most frequently used iterative algorithm in nuclear medicine applications is the MLEM algorithm. [10,11] This last one solves a set of linear equations, assuming Poisson noise is present in the projection data. A unique property of the MLEM algorithm is that it produces an image with non-negative pixel values.
Problem of attenuation in SPECT images
Description of physical effects:
Transmission of photons (gamma photons) through any material can be characterized by the linear attenuation coefficient μ, which depends on the photon energy E and the atomic number Z of the material. [11] The linear attenuation coefficient can be defined as the probability per unit path length that the photon will interact with the absorber (for example, patient tissue). Attenuation is more important as the probability of interaction is high. It is proportional to this probability and is expressed in cm-1. [2] The number of photons decreases in time according to an exponential law. It is modeled mathematically by the relation:
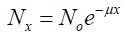 (1)
(1)
Where N0 is the number of initial photons and N the number of photons after the interaction, x is the thickness traversed by the photon. μ is the linear attenuation coefficient, grouping the contribution of the various attenuation processes. As we said previously, the linear attenuation coefficient μ depends on the photon energy E and materials. At 140 keV and for biological materials, Compton scattering in the predominant effect.
Influence of attenuation on SPECT images
Effects of attenuation on the quality of the image are:
• Loss of a huge number of photons which conducts to a decrease in SNR (e.g in thoracic SPECT, 10% of the emitted photons at the level of the heart quit the patient);
• Poor quantification (i.e in SPECT, attenuation conducts to activity underestimate generally greater than 70%);
• As the attenuation is uneven depending on the depth, it also considerably changes the image’s aspect (i.e harmful to the detection of deep lesions). [12]
To provide a quality image, it is necessary to correct the attenuation. It exists many methods in the literature.
Attenuation correction methods
Various methods are used to rectify the attenuation in SPECT images. They can be classified into three main approaches: before tomographic reconstruction (pre-correction), after tomographic reconstruction (post-correction) and during tomographic reconstruction (iterative methods).
Tavakoli et al. [13] utilized iterative and post-correction methods to rectify the attenuation in SPECT images. The SPECT images were reconstructed using both FBP and iterative OSEM reconstruction methods. They were applied in a heart phantom of 64 × 64 matrix size. This attenuation correction improves the accuracy of both methods FBP and OSEM.
Patton et al. [14] utilized iterative methods to rectify the attenuation. Iterative methods introduce the correction during reconstruction. Images were reconstructed using an iterative reconstruction algorithm (OSEM with 2 iterations). SPECT scans were corrected for attenuation using CT data. This method was applied on a cylindrical phantom and on a thorax phantom. An additional benefit of this techno-logic advance is that anatomic images can be used to perform high-quality attenuation corrections of the radio-pharmaceutical distribution. Tavakoli et al., [15] also, utilized an iterative method to rectify the attenuation. In their work, SPECT images are reconstructed using an MLEM iterative algorithm. The attenuation map is created by a scaling curve obtained for 140 kVp CT images with a small scan field-of-view. The attenuation map is incorporated into the reconstruction. CT images are reconstructed using the FBP furnished by the scanner vendor. This technique was applied to small pigs in myocardial perfusion studies. Here, by this method, attenuation correction increased the image-derived myocardial radionuclide concentration from 16% to 35%. All methods described above correct the attenuation slice by slice. Although, compared with slice-by- slice approaches for SPECT reconstruction, three-dimensional iterative methods furnish a more accurate physical model and an improved SPECT image. [3,4,15]
Proposed method
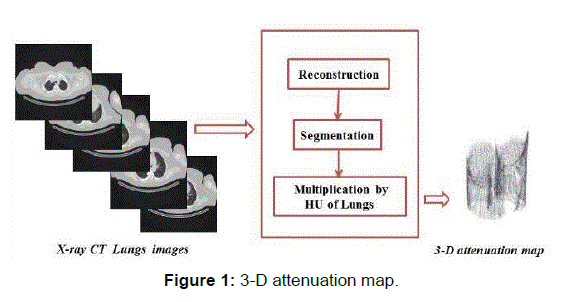
In this paper, we present new 3D-map attenuation correction for SPECT image quality enhancement. The map attenuation is created by three steps:
Step 1: The reconstruction of CT lung images are done by FBP;
Step 2: The lungs are extracted using Otsu’s thresholding;
Step 3: The segmented image was multiplied by the HU of the lung to obtain the attenuation map.
The Hounsfield unit (HU) scale is a linear transformation of the original linear attenuation coefficient measurement into one in which the radiodensity of distilled water at standard pressure and temperature (STP) is defined as zero HU, while the radiodensity of air at STP is defined as -1000 HU. In a voxel with average linear attenuation coefficient μ, the corresponding HU value is therefore given by:
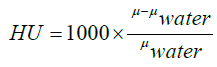 (2)
(2)
Where μwater is the linear attenuation coefficient of water. The HU of the lung is between -500 and -700 HU. [12] The steps described below are applied to all slices (CT images). And from these slices, we will provide the volume of the map. The 3-D attenuation map is presented in Figure 1.
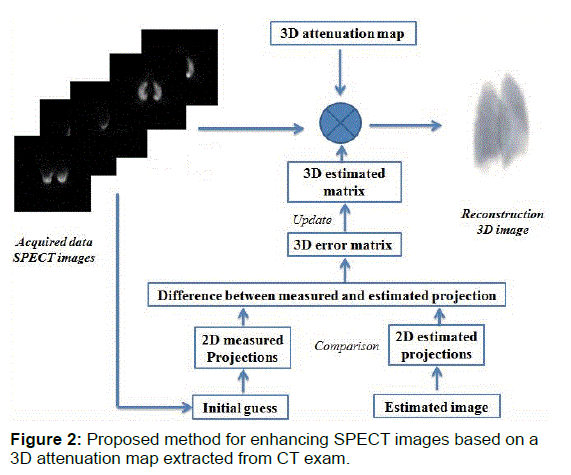
After the creation of 3-D attenuation map, the CT derived 3-D attenuation map is used to reconstruct the SPECT images with a three-D MLEM (3-D ML-EM) iterative algorithm using 25 iterations. The 3-D MLEM allows the reconstruction of all slices simultaneously.ML-EM algorithm is [17]
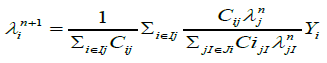 (3)
(3)
Where 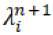 is the estimated source intensity at voxel j at iteration n, Yi is the number of recorded counts in projection bin i and Cij, the system matrix value for the i, j elements, is the probability that a photon emitted from voxel j gets detected in projection bin i.
is the estimated source intensity at voxel j at iteration n, Yi is the number of recorded counts in projection bin i and Cij, the system matrix value for the i, j elements, is the probability that a photon emitted from voxel j gets detected in projection bin i.
In fully 3D reconstruction, detection probabilities are considered for all combinations of i and j. In order to express approximate 3D reconstruction, Ij and Ji are used, where Ij is the set of projection bins to which the voxel j contributes, and Ji is the set of voxels which contribute to projection bin i.
The principle of the proposed method is described in Figure 2.
Results and Discussion
Data base
The proposed method is applied to 21 thoracic SPECT exams (128 × 128 × 66).They taken on the radiology department of Salah Azaiez Institut in Tunisia. The X-ray and gamma-ray data were obtained from a hybrid machine combining an X- ray CT scanner and a dual-headed SPECT scanner juxtaposed to enable systematic registration of SPECT and X-ray CT images. The principle of this imaging is based on the injection of 1.5 mCi of 99mTc−MAA (macro aggregated human serum albumin) which is subsequently acquired according to different incidences (ant, post...) completed in some cases by SPECT/CT (low dose).
Evaluation parameters
Four different parameters are used to compare the different results in this work. They are the Image Quality Index, mean square error (MSE), peak signal-to-noise ratio (PSNR) and structural similarity index (SSIM). Results of these parameters are presented in Table 1.
| Methods/Metrics | MSE | PSNR | SSIM | Image Quality Index |
|---|---|---|---|---|
| Attenuation correction after tomographic reconstruction [18] | 113.080 | 21.605 | 0.331 | 0.626 |
| Attenuation correction during image reconstruction using iterative method ART [17] | 195.685 | 19.231 | 0.352 | 0.680 |
| 3-D slice by slice reconstruction [22] | 113.873 | 21.784 | 0.156 | 0.701 |
| Proposed method | 101.388 | 22.084 | 0.525 | 0.892 |
Table 1: Evaluation parameters.
Image Quality Index:
The image quality index is determined using [6]:
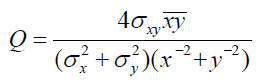 (4)
(4)
Where x and y are mean pixel values of the test and reference images, σx and σy are standard deviation of test and reference images,
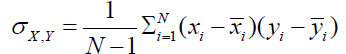 (5)
(5)
Mean square error:
MSE is defined as the average of squares of errors between the original image and the reconstructed one. It is defined by [5]:
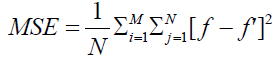 (6)
(6)
Where f’ is the reconstructed image and f is the original image, M and N are the dimension of these images.
Peak signal-to-noise ratio:
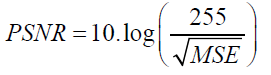 (7)
(7)
Structural similarity index:
It has been developed to measure the visual quality of a compressed image, compared to the original image one. The idea of SSIM is to measure the similarity of structure between the two images, rather than a pixel-to-pixel difference. [19] The general form of the SSIM index is defined as:
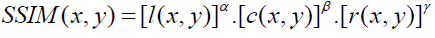 (8)
(8)
Where α, β, and γ are parameters that define the relative importance of each component. SSIM (x, y) ranges from 0 (completely different) to 1 (identical patches). Finally, a mean SSIM index is computed to evaluate the global image similarity.
Dunnett test:
The Dunnett test is a post-Hoc Test. It compares averages of several experimental groups with those of a control group, in order to evaluate the difference. [20] When an ANOVA test has significant findings, it doesn’t report which pairs of means are different. Dunnett’s can be used after the ANOVA has been run to identify the pairs with significant differences. [21] A p-value < 0.05 is considered statistically significant. Results of several tests are presented in Table 2.
| Methods /Proposed method | p(MSE) | p(PSNR) | p(SSIM) | p(Image Quality Index) |
|---|---|---|---|---|
| Attenuation correction after tomographic reconstruction [18] |
0.001 | 0.021 | 0.000 | 0.022 |
| Attenuation correction during image reconstruction Using iterative method ART [17] |
0.002 | 0.003 | 0.000 | 0.013 |
| 3-D slice by slice reconstruction [22] | 0.036 | 0.000 | 0.01 | 0.0045 |
Table 2: Multiple comparisons: Dunnett “TEST T”.
Discussion
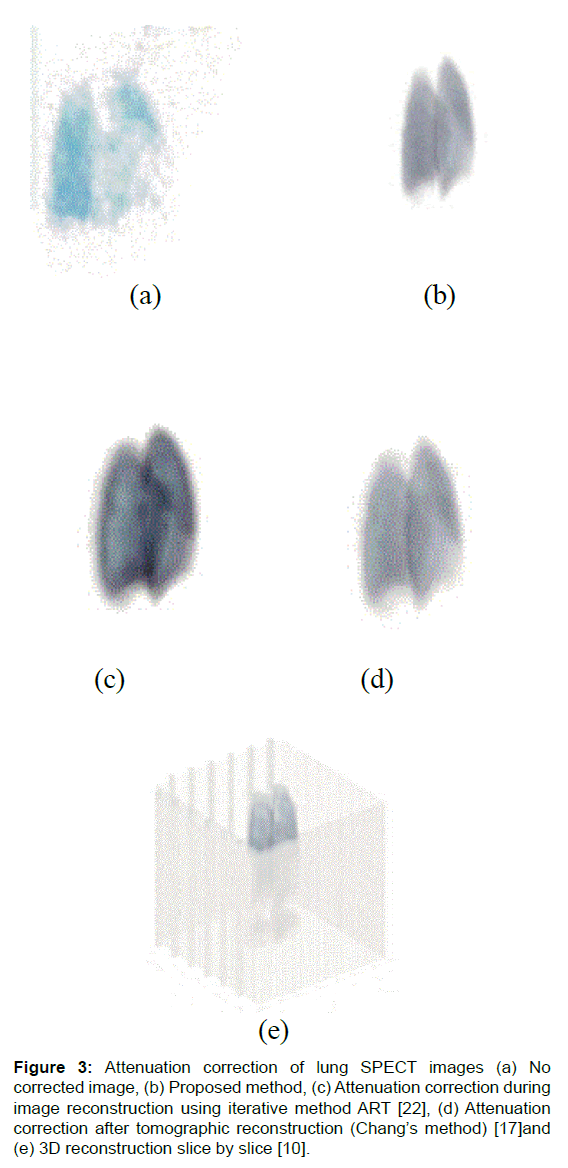
The proposed method is, first, compared to the 3-D reconstruction slice by slice. In this method, the attenuation correction is realized in a 2-D image for all slices. [10] Then the combination between all slices has formed a 3-D image. The proposed method is compared also with two other methods: an iterative method [22] and an analytic one. [17] Results of these methods are shown in Figure 3. Visually, from this image, we can observe that the image corrected by the proposed method is better than images corrected by the other algorithms.
Figure 3: Attenuation correction of lung SPECT images (a) No corrected image, (b) Proposed method, (c) Attenuation correction during image reconstruction using iterative method ART [22], (d) Attenuation correction after tomographic reconstruction (Chang’s method) [17] and (e) 3D reconstruction slice by slice [10].
The results of the Image Quality Index, PSNR, MSE, and SSIM are presented in Table 1. From this table, we can conclude that the value of Image Quality Index of the proposed method (0.892) is better than those of Nasr et al. (0.680), Onishi et al. (0.626) and 3-D reconstruction slice by slice (0.701).
The value of the PSNR of the proposed method is 22.84. It is also higher than those obtained by Onishi et al. method, Nasr et al. method and 3-D reconstruction slice by slice method that are respectively 21.605, 19.231 and 21.784. The lower value of the MSE (101.388) is obtained by the proposed method. It is twice time lower than the value of Nasr et al. (195.685). It is also lower than values of Chang’s and 3-D reconstruction slice by slice methods. SSIM value of the proposed method is 0.525. It is higher than values of SSIM obtained by Onishi et al. method, Nasr et al. method and 3-D reconstruction slice by slice method that are respectively 0.331, 0.352 and 0.156. From these results, we can conclude that our proposed method improves the accuracy, the PSNR, and the SSIM and it minimizes the MSE.
In the end, it has to help the practitioner by higher better highlighting objects of interests or facilitating the automatic extraction of characteristic features.
In order to verify that there is a significant difference between the means of performance parameters of the proposed method and those of other methods, we used the Dunnett test. Results of these tests are presented in Table 2. Values of p for MSE, PSNR, SSIM and Image Quality Index are less than 0.05 for all methods. Therefore, we can conclude that the difference between the means of these parameters is significant. These results confirm the superiority of the proposed method.
In order to verify that there is a significant difference between the means of performance parameters of the proposed method and those of other methods, we used the Dunnett test. Results of these tests are presented in Table 2. Values of p for MSE, PSNR, SSIM and Image Quality Index are less than 0.05 for all methods. Therefore, we can conclude that the difference between the means of these parameters is significant. These results confirm the superiority of the proposed method.
Conclusion
In this paper, we proposed a new 3-D map for attenuation correction of Lung SPECT images. In fact, after extracting lungs regions from X-ray CT images and multiplying it by lungs HU, SPECT images are reconstructed by 3-D MLEM algorithm combined to the 3-D proposed map. This proposed method presents well good results. Its validation is confirmed by comparing it to Onishi’s, Nasr’s and 3-D reconstruction slice by slice methods. It gives the best values of accuracy, SSIM, PSNR, and MSE. Means of metrics of the proposed method are significantly different from those of other methods (p < 0.05). This proves the efficiency of the proposed method in attenuation correction of SPECT images.
Competing Interests
The authors declare that they have no competing interests.
References
- Patton JA, Turkington TG. SPECT/CT physical principles and attenuation correction. Journal of nuclear medicine technology. 2008;36:1-0.
- Gedik GK, Sari O. Influence of single photon emission computed tomography (SPECT) reconstruction algorithm on diagnostic accuracy of parathyroid scintigraphy: Comparison of iterative reconstruction with filtered backprojection. The Indian journal of medical research. 2017;145:479.
- Greffier J, Macri F, Larbi A, Fernandez A, Pereira F, Mekkaoui C, et al. Dose reduction with iterative reconstruction in multi-detector CT: what is the impact on deformation of circular structures in phantom study?. Diagnostic and interventional imaging. 2016;97:187-196.
- Beekman FJ, de Jong HW, van Geloven S. Efficient fully 3-D iterative SPECT reconstruction with Monte Carlo-based scatter compensation. IEEE transactions on medical imaging. 2002;21:867-877.
- Kinahan PE, Hasegawa BH, Beyer T. X-ray-based attenuation correction for positron emission tomography/computed tomography scanners. InSeminars in nuclear medicine 2003;33:166-179.
- Wang Z, Bovik AC. A Universal Image Quality Index. IEEE Signal Processing Letters, 2002;9:81-84.
- Andersen AH, Kak AC. Simultaneous algebraic reconstruc- tion technique (SART): a superior implementation of the ART algorithm. Ultrasonic imaging, 1984;6:81-94.
- Bruyant PP. Analytic and iterative reconstruction algorithms in SPECT. Journal of Nuclear Medicine, 2002;43:1343-1358.
- Alzimami KS, Sassi SA, Spyrou NM. A comparison between 3D OSEM and FBP image reconstruction algorithms in SPECT. In Advances in Electrical Engineering and Computational Science, 2009;195-206.
- Romdhane H, Cherni MA, Sellem DB. New Attenuation Map for SPECT Images Quality Enhancement. In 2018 5th International Conference on Control, Decision and Information Technologies (CoDIT), 2018;731-736.
- Kheruka SC, Aggarwal LM, Sharma N, Naithani UC, Maurya K, Gambhir S. Evaluation of single-photon emission computed tomography images obtained with and without copper filter by segmentation. Indian journal of nuclear medicine: IJNM: the official journal of the Society of Nuclear Medicine, India, 2016;31:114.
- Ella A. Kazerooni Barry H. Gross. The core curriculum: Cardiopulmonary imaging (the core curriculum series),” Amazon, Ed. LWW; 1 edition, 2003.
- Shepp LA, Vardi Y. Maximum likelihood reconstruction for emission tomography. IEEE transactions on medical imaging, 1982;1:113-122.
- Onishi H, Sakai T, Shiromoto O, Amijima H. Validation of Optimum ROI Size for 123I-FP-CIT SPECT Imaging Using a 3D Mathematical Cylinder Phantom. Asia Oceania Journal of Nuclear Medicine and Biology, 2018;6:139.
- Tavakoli M, Neij M. Quantitative evaluation of the effect of attenuation correction in SPECT images with CT-derived attenuation. InMedical Imaging 2019: Physics of Medical Imaging 2019;10948.
- Wieczorek H. The image quality of FBP and MLEM recon- struction. Physics in Medicine Biology, 2010;55:3161.
- Kadrmas DJ, Frey EC, Karimi SS, Tsui BM. Fast implementations of reconstruction-based scatter compensation in fully 3D SPECT image reconstruction. Physics in Medicine Biology, 1988;43:857.
- Zeng GL. Image reconstruction—a tutorial. Computerized medical imaging and graphics, 2001;25:97-103.
- Renieblas GP, Nogue´s AT, Gonza´lez AM, Leo´n NG, del Castillo EG. Structural similarity index family for image quality assessment in radiological images. Journal of Medical Imaging, 2017;4:035501.
- Herberich E, Sikorski J, Hothorn T. A robust procedure for comparing multiple means under heteroscedasticity in unbalanced designs. PloS one 2010.
- Kim HY. Statistical notes for clinical researchers: post-hoc multiple comparisons. Restorative dentistry endodontics, 2015;40:172-176.
- Nasr E. Accurate attenuation correction for algebraic recon- struction technique in SPECT. Journal of Computational Mathematics, 2010;28:401-417.



 The Annals of Medical and Health Sciences Research is a monthly multidisciplinary medical journal.
The Annals of Medical and Health Sciences Research is a monthly multidisciplinary medical journal.