Estimation of Stature from Arm Span in Medical Students of Maharashtra, India
- *Corresponding Author:
- Dr. Bagul AS
Department of Pediatrics, Government Medical College, Nagpur - 440 003, Maharashtra, India.
E-mail: drabhaybagul@gmail.com
Abstract
Background: Stature can be estimated from body parameters in dead and mutilated bodies using regression equation or multiplication factor. However, regression equations and multiplication factors are specific for the region only and can’t be used in all population. Aim: To formulate regression equation and multiplication factor for the estimation of stature from arm span (AS) for a region in Maharashtra, India. Subjects and Methods: It was a cross‑sectional study, did over a period of 2 years, from October 2011 to September 2013. Four hundred students of three Government medical colleges of Maharashtra, aged 18–24 years were enrolled in the study. Stature and AS were measured and subjected to statistical analysis. Unpaired t‑test and simple linear regression were used. Results: Stature and AS of 400 medical students (219 males and 181 females) were measured. Subjects were divided into six groups depending upon age. Simple regression equation and multiplication factor for male and female and for each age group were derived for estimation of stature. We found correlation coefficient (R) of 0.89 in male and 0.90 in female using simple regression, which shows strong correlation between stature and AS. Conclusion: Mean stature and AS of male were more than female with statistical significance. Stature can be accurately estimated from AS using simple regression equation or multiplication factor.
Keywords
Arm span, Simple regression, Stature
Introduction
“Identification is an individual’s birth right” United Nations Declaration on Human Rights dated December 10, 1948.[1] Identification is more important in dead unknown bodies and mass disaster like explosion, railway and aircraft accidents, where only parts of bodies might be available. Apart from identification, stature measurement is required for assessment of children’s growth,[2] calculation of nutritional indices,[3] for prediction and standardization of physiological parameters such as lung volumes,[4] muscle strength,[5] glomerular filtration rate,[6] and resting metabolic rate[7] and for adjustment of drug dosage.[8] However, in some cases, measurement of stature is difficult or impossible due to deformities of the trunk or legs, lower limb amputation, fractures or contractures or in patients who are unable to stand.[9]
Dimensional relationship between body segments and the whole body has been the focus of scientist, anatomist and anthropologist for many years.[10] For this purpose, many sets of regression equation have been developed, and the better known are Karl Pearson, Trotter and Glesser from western countries and Pan (1924), Singh and Sohal (1952), and Mehat and Thomas were from India.[11] Previous studies have reported the effectiveness of using various body parameters in estimating stature and the arm span (AS) was found to be the most reliable.[12,13] Inter-population comparison and estimation of stature from these formulae are not appropriate, as climate, heredity, nutritional status of the population has been reported to have an effect on stature. In a country like India where racial and ethnic variations are well known, the region-wise study seems to be necessary.
Present study was planned to formulate regression equation and multiplication factor for the estimation of stature from AS in medical students of Vidarbha region of Maharashtra.
Subjects and Methods
It was a cross-sectional study, did over a period of 2 years, from October 2011 to September 2013. By simple random sampling, four hundred students (219 males and 181 females) of three Government Medical Colleges of Maharashtra, India, aged 18–24 years were enrolled in the study after taking informed consent. The students who are born and brought up in a specific region of ancestral origin from this region are the target population. Students with deformity of limb or vertebral column were excluded. The study was approved by the Ethical Committee.
Following measurements were taken:
Stature (standing height)
The subject was asked to stand barefoot on the base of a standard stadiometer in a standard standing position. The individual was instructed to stand barefoot, heels are slightly separated, and weight is borne evenly on both feet. Heels, buttocks and back are brought in contact with a vertical surface. The head is so positioned that the subject looks directly forward with the Frankfurt plane (the line joining the floor of external auditory meatus to the lower margin of the orbit) and biauricular plane being horizontal. The headpiece of stadiometer is kept firmly over the vertex to compress the hair and height is then measured.[14]
Arm span
Arm span was measured with a flexible steel tape from the tip of the middle finger on one hand to the tip of the middle finger on the other hand with the individual standing with back to the wall with both arms abducted to 90° the elbows and wrists extended and the palms facing directly forward.[15] AS measurement includes the shoulder width.[16] Readings were taken to the nearest 0.1 cm.
Observations were recorded in a predesigned pretested proforma. All these measurements were taken by the single author to avoid inter-observer bias and were measured at a fixed time to avoid diurnal variation. All the above measurements were tabulated and subjected to statistical analysis.
As there was no Indian study to guide about sample size, assumption is made on the pilot study conducted on 50 subjects to calculate sample size. Required sample size for male is 195 and for female 174. Power of the study is 80%.
The measurements obtained were statistically analyzed using Stata version 10.0 (Texas, USA), a data analysis and statistical software. All measurement variables were presented with mean (standard deviation [SD]) and 95% confidence intervals (CI). Analysis of the differences in stature and AS, between male and female subjects was done by unpaired t-test. Karl Pearson’s correlation coefficients are derived between variables AS and stature, and standard error and coefficient of determination (R2) was calculated. Single linear regressions were done to estimate stature from AS. Multiplication factor is calculated. Multiplication factor is the ratio of the stature to the respective physical measurements. All the tests were 2 sided and P < 0.05 was considered as statistical significance.
Results
Enrolled subjects (400), both males (54.7%, 219/400) and females (45.2%, 181/400), were divided according to age in six groups as 18–19, 19–20, 20–21, 21–22, 22–23, 23–24 years.
It is revealed that the stature in males ranged from 142.0 cm to 187.0 cm with mean (SD, 95% CI) of 170.75 cm (9.47, 8.856–10.175). The stature in females ranged from 141.10 cm to 186.00 cm with mean (SD, 95% CI) of 159.46 cm (7.66, 7.163–8.231). It is observed that males have greater stature than females, and it was statistically significant (P < 0.001, 95% CI 9.576–13.003). In males, the AS ranged from 143 cm to 194 cm with a mean (SD, 95% CI) of 172.93 cm (9.32, 8.716–10.014). In females, the AS ranged from 141 cm to 186.6 cm with a mean (SD, 95% CI) of 162.09 cm (8.88, 8.304–9.541). The AS was more in males than females, and it was statistically significant (P < 0.001, 95% CI = 9.038–12.641).
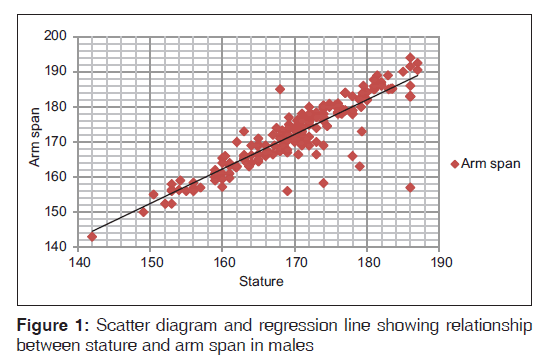
Linear regression equations were derived for each age group and for total males separately for estimation of stature from AS [Table 1]. In males, AS showed high positive value of correlation coefficient (>0.8) which suggest a strong positive correlation between stature and AS [Figure 1]. Standard error for the total is ± 3.82. The equation derived for total males can be used within the predictive range (R2) of ± 0.79 for AS.
| Age group | Number of subjects | Regression equation | SE | R | R2 |
|---|---|---|---|---|---|
| 18-19 | 42 | S=39.02+0.76 AS | 3.68 | 0.87 | 0.76 |
| 19-20 | 74 | S=47.69+0.77 AS | 4.95 | 0.80 | 0.64 |
| 20-21 | 64 | S=17.27+0.89 AS | 3.16 | 0.93 | 0.86 |
| 21-22 | 21 | S=18.26+0.83 AS | 1.88 | 0.98 | 0.97 |
| 22-23 | 13 | S=5.97+0.94 AS | 1.25 | 0.98 | 0.97 |
| 23-24 | 5 | S=3.98+0.95 AS | 0.82 | 0.99 | 0.99 |
| Total | 219 | S=31.26+0.806 AS | 3.82 | 0.89 | 0.79 |
SE: Standard error, R: Correlation coefficient, R2: Coefficient of determination, AS: Arm span in centimeter
Table 1: Regression equation for estimating height from AS in males in various age groups
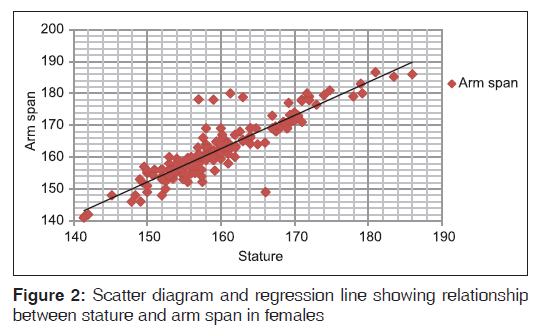
Linear regression equations were derived for each age group and for total females separately for estimation of stature from AS [Table 2]. In females, AS showed high positive value of correlation coefficient (>0.8), which suggest a strong positive correlation between stature and AS [Figure 2]. As subjects were very less in two age groups (22–23 and 23–24 years), regression equation could not be derived. The equation derived for total females can be used within the predictive range (R2) of ± 0.81 for AS.
| Age group | Number of subjects | Regression equation | SE | R | R2 |
|---|---|---|---|---|---|
| 18-19 | 46 | S=52.49+0.65 AS | 3.68 | 0.87 | 0.76 |
| 19-20 | 101 | S=25.89+0.82 AS | 3.43 | 0.91 | 0.83 |
| 20-21 | 25 | S=43.03+0.72 AS | 3.47 | 0.87 | 0.77 |
| 21-22 | 5 | S=3.62+0.965 AS | 1.14 | 0.99 | 0.98 |
| Total | 177 | S=33.54+0.77 AS | 3.32 | 0.90 | 0.81 |
SE: Standard error, R: Correlation coefficient, R2: Coefficient of determination, AS: Arm span in centimeter
Table 2: Regression equation for estimating height from AS in females in various age groups
Regression equation for estimation of stature from AS in male is S = 31.25 + 0.80 AS, and in female is S = 33.54 + 0.77 AS. Multiplication factor were derived for estimation of stature from AS. Multiplication factor for male was 0.99 and for female was 0.98, and SD was 0.02. If AS is multiplied by the respective multiplication factor, the approximate stature of an individual can be estimated.
Discussion
Stature is a parameter that can be established even in mutilated and dismembered bodies, as well as in fragmentary remains. AS can be used for estimation of stature in living subjects also, in whom, it is not possible to measure the stature due to deformity.
In the present study, a total of 400 (219 males and 181 females) medical students between the age of 18 and 24 years were enrolled. Since maximum height of an individual is attained between 18 and 24 years, these individuals were selected for the study. Recently published studies [17-19] also enrolled subjects of same age group. A study from Thailand [20] has reported the decrease in the correlation between AS and stature with increasing age, as stature decreases with age and AS doesn’t. Although earlier study[15] found contribution of age is insignificant in estimation of stature, we have considered age and regression equations are derived for different age groups.
All the human beings belong to the same species, that is, Homo sapiens. No two individuals are exactly alike in all their measurable traits, even genetically identical twins (monozygotic) differ in some respects. These traits tend to undergo change from birth to death, in health and disease, and since skeletal development is influenced by a number of factors producing differences in skeletal proportions between different geographical areas. This explains the difference in anthropometric measurements in different geographical areas.
We observed that males have greater stature than females. This can be explained by genetic constitution of males. Age of puberty being 2 years later in males as compared to females give them additional time for growth. This suggests that the formula for one sex cannot be applied to estimate stature for other sex. The stature found by different authors[13,21,22] in India in different region or state is different than the present study. Author[22] from Chandigarh found mean (SD) stature of male was 168.2 (6.5) and of female was 155 (5.2) and this can be explained by different genetic constitution, environmental factors and nutrition in different population groups.
Mean AS in male was more than female, and it was statistically significant (P < 0.001). So, the same regression equation can’t be used in both sexes to estimate stature. We formulate regression equation for estimation of stature depending upon sex and age. We found a correlation coefficient (R) of 0.89 in male and 0.90 in female, which shows strong correlation between stature and AS and it was similar to published studies.[13,23] Published study from Iran[24] reported that height estimated from AS performs much better than AS, to predict pulmonary function parameters. So, these regression equations can be used.
When multiplication factors are used to estimate stature, we found SD of 0.02 for AS. So, AS can be used to estimate stature of the person with accuracy using the multiplication factor. Although multiplication factor is frequently used by authors[15] to estimate stature from body parameter, the error of estimate is usually large whenever multiplication factor method is used, and it is well explained by the previous study.[22]
In present study, medical students of Government Medical College were enrolled which are from middle to higher socioeconomic class. So, the anthropometric measurements can be on higher side, when compared to the general population. Ideal study to formulate regression equation for all population should be a community-based study. A range is the only thing that can be accurately determined from a formula. In addition, these equations cannot be applied for giants and dwarfs.
Conclusion
Stature of male was 170.75 (9.43) cm, and it was more than female [159.46 (±7.66) cm] with statistical significance. Similarly, AS of male was more than female. We found correlation coefficient (R) of 0.89 in male and 0.90 in female using simple regression, which shows strong correlation between stature and AS. Stature can be accurately estimated from AS using simple regression equation or multiplication factor
References
- Universal declaration of human rights. [Place unknown]: United Nations. Available from: http://www.un.org/en/ documents/udhr/index.shtml. [Last cited on 2013 Sep 20].
- WHO Multicentre Growth Reference Study Group. WHO Child Growth Standards: Length/height-for-age, weight-for-age, weight-for-length, weight-for-height and body mass index-for-age: Methods and development. Geneva: World Health Organization; 2006.
- Heymsfield SB, Gallagher D, Mayer L, Beetsch J, Pietrobelli A. Scaling of human body composition to stature: New insights into body mass index. Am J Clin Nutr 2007;86:82-91.
- Pellegrino R, Viegi G, Brusasco V, Crapo RO, Burgos F, Casaburi R, et al. Interpretative strategies for lung function tests. Eur Respir J 2005;26:948-68.
- Hogrel JY, Decostre V, Alberti C, Canal A, Ollivier G, Josserand E, et al. Stature is an essential predictor of muscle strength in children. BMC Musculoskelet Disord 2012;13:176.
- Schwartz GJ, Muñoz A, Schneider MF, Mak RH, Kaskel F, Warady BA, et al. New equations to estimate GFR in children with CKD. J Am Soc Nephrol 2009;20:629-37.
- Frankenfield D, Roth-Yousey L, Compher C. Comparison of predictive equations for resting metabolic rate in healthy nonobese and obese adults: A systematic review. J Am Diet Assoc 2005;105:775-89.
- Kaestner SA, Sewell GJ. Chemotherapy dosing part I: Scientific basis for current practice and use of body surface area. Clin Oncol (R Coll Radiol) 2007;19:23-37.
- Rajkumar CM, Tomar S, Ashoka R. The relationship between arm span and height in adult males of north Indian Punjabi population. J Evol Med Dent Sci 2013;2:332-9.
- Mukherjee JB, editor. Personal identification. In: Forensic Medicine and Toxicology. 2nd ed. New Delhi: Arnold Associates; 1994. p. 128-9.
- Bass WM. Anthropology. In: Siegel JA, editor. Encyclopedia of Forensic Sciences. Vol. 1. London: Academic Press; 2000. p. 194-284.
- Yabanci N, Kiliç S, Simsek I. The relationship between height and arm span, mid-upper arm and waist circumferences in children. Ann Hum Biol 2010;37:70-5.
- Mohanty SP, Babu SS, Nair NS. The use of arm span as a predictor of height: A study of South Indian women. J Orthop Surg (Hong Kong) 2001;9:19-23.
- Ghai OP, Jain V, Sankhayan N, Agarwal R. Normal growth and its disorder. In: Ghai OP, Paul VK, Bagga A, editor. Essential Paediatrics. 7th ed. New Delhi: CBS Publishers and Distributors Pvt. Ltd.; 2009. p. 5.
- Hossain S, Begum JA, Akhter Z. Measurement of stature from arm span – An anthropometric study on Garo Tribal Bangladeshi females. Banglad J Anat 2011;9:5-9.
- Mazicioglu MM, Hatipoglu N, Ozturk A, Gun I, Ustunbas HB, Kurtoglu S. Age references for the arm span and stature of Turkish children and adolescents. Ann Hum Biol 2009;36:308-19.
- Agnihotri AK, Agnihotri S, Jeebun N, Googoolye K Prediction of stature using hand dimensions. J Forensic Leg Med 2008;15:479-82.
- Rajkumar CM. The relationship between hand breadth and height in adult males of north Indian Punjabi population. J Evol Med Dent Sci 2013;2:1880-7.
- Krishna K. Estimation of stature from footprint and foot outlines dimensions in Gujjars of North India. Forensic Sci Int 2007;14:1-9.
- Manonai J, Khanacharoen A, Theppisai U, Chittacharoen A. Relationship between height and arm span in women of different age groups. J Obstet Gynaecol Res 2001;27:325-7.
- Varun R, Jayasinghearachchi TM, Priyalini R, Gunasena MD. Arm span and knee height as predictors of stature among Peradeniya medical students. Sri Lankan J Anaesthesiol 2011;19:76-80.
- Krishan K, Kanchan T, Sharma A. Multiplication factor versus regression analysis in stature estimation from hand and foot dimensions. J Forensic Leg Med 2012;19:211-4.
- Aggarwal AN, Gupta D, Ezekiel LM, Jindal SK. Statistical estimation of height from arm span in north Indian subjects. Indian J Physiol Pharmacol 2000;44:329-34.
- Golshan M, Amra B, Hoghoghi MA. Is arm Span an accurate measure of height to predict pulmonary function parameters? Monaldi Arch Chest Dis 2003;59:189-92.



 The Annals of Medical and Health Sciences Research is a monthly multidisciplinary medical journal.
The Annals of Medical and Health Sciences Research is a monthly multidisciplinary medical journal.