Reliability of Various Modified Demirjian Methods for Age Estimation in South Indians – A Retrospective Digital Orthopantomographic Study
2 Department of Dentistry, Rangaraya medical college, Kakinada, East Godavari, India
3 Department of Oral Medicine & Radiology, Vishnu Dental College, Bhimavaram, West Godavari, Andhra Pradesh, India, Email: dr.rizwanamds@gmail.com
4 Department of Periodontics, GSL Dental College & Hospital Rajamundry, East Godavari, Andhrapradesh, India
5 Department of Oral Medicine & Radiology, Government Dental College & Hospital, Hyderabad, Telangana, India
6 Department of Prosthodontics, Malabar Dental College and Research centre, Edappal, Malappuram, Kerala, India
Citation: Thetay AAR, et al. Reliability of Various Modified Demirjian Methods for Age Estimation in South Indians - A Retrospective Digital Orthopantomographic Study. Ann Med Health Sci Res. 2017; 7: 88-95
This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com
Abstract
Introduction: Demirjian’s dental maturity scores are widely used to assess dental maturity and estimate age. Various authors revised Demirjian’s method by adapting Demirjian’s stages and proposed new data for age estimation. The present study aimed to assess the age using original and modified Demirjian methods from the reference data and also to correlate dental age with chronological age. Materials and methods: In the target sample of 660 dental radiographs of age 6-16.99 years, seven mandibular permanent teeth (Central incisor I1 to Second molar M2) were assessed and dental age was calculated using four maturity scales and ten methods that use data for individual teeth. The mean difference between dental age (DA) and chronological age (CA) was calculated as well as other measures of accuracy such as mean obsolute difference (MAD), percentage aged to within six months and to within 10% of age. Results: The method that performed best was the dental maturity scale of Willems I et al .(highest percentage of individual aged to within 0.5 years of real age) with MAD of 1 year, followed by Original Demirjian method with MAD of 1.06 years and Willems II method with MAD of 1.1 years. Conclusion: The present study showed that original Demirjian’s method was found to be highly accurate followed by Willems I method. Thirdly, Willems II method was better followed by Chaillet et al. method. All the fourteen methods assessed were found to reliable for age estimation in South Indians.
Keywords
Dental age estimation; Demirjian’s method; Forensic dentistry; Demirjian stages
Introduction
Estimating age of an unknown individual has become a challenge for a variety of reasons such as criminal and legal issues, for social issues like birth certificate, marriage, applying for job and retirement. Age can be better estimated by observing the tooth formation. Ideally accuracy of dental age estimation can be increased by applying known different methods available in the literature and performing repetitive measurements and calculations. [1]. No two children of the same calendar age will have similarity in their tooth development.
Dental maturity can be quantified by describing the age of tooth stages of individual teeth. Three approaches describe radiographic dental development: 1. Age at attainment of a developmental tooth stage (mean age entering a tooth stage, adapted maturity data) 2. Age at a stage of tooth development (within stage) 3. Age at a stage of maturation of a set of teeth (maturity scales). All the three types of data are important in dentistry because clinicians must assess growth; avoid treatments that may damage developing teeth during critical situations and also to assess unknown age of patients. [2].
Mean age can be calculated either using cumulative distribution frequency (mean age entering a stage) or conventional statistics (mean age with in a stage). Mean age of entry for a tooth stage indicates the age when half of children at that age, have reached or passed the stage and was found to be better in comparing tooth maturation between groups. Adapted maturity data was obtained for each stage of developing tooth by adding half the interval to the next stage. Mean age with in a stage represents the average age of individuals who have entered one stage but not the subsequent stage and was calculated as the 51% confidence interval of age for each individual tooth stage. [2,3].
Since 50 years, numerous dental maturity studies have been reported to estimate age. Demirjian’s (DM) dental maturity method is a useful tool to assess tooth maturation in children and these standards may not be valid in other populations and also not suitable to compare maturity at group level. [4]. Moreover studies done on other populations showed a greater variability in the dental maturation process for different populations. [5]. So various authors [6-9]. revised Demirjian’s method by adapting Demirjian’s stages and proposed new data for age estimation. Willems G et al. developed gender specific [6]. and new nongender- specific [9]. dental maturity scores from Belgian- Caucasian sample. Liversidge et al. [10]. assessed the timing of Demirjian tooth stages of individual teeth in children from eight countries (Finland, Sweden, England, Korea, Belgium, Australia, Canada, France) and provided data for mean age of tooth formation stages and mean age of a child with in a stage and also concluded that no major differences were observed in the timing of tooth formation stages in the selected sample. Chaillet et al. [7]. introduced adapted dental development tables using Demirjian’s stages and provided international dental age estimation standards when ethnic origin was not known.
Liversidge [3]. assessed the timing and variation of individual permanent mandibular teeth using Demirjian stages in 4710 males and 4661 females of age 2-18 years and presented data for each tooth stage in three ways as mean age entering Demirjian stages, adapted maturity data for age prediction and average age within stage from uniform age distribution sample for males, females and pooled sex. Nystrom et al. [8]. assessed the timing of development in individual mandibular teeth using Demirjian’s stages in Finns of 966 males and 1004 females from birth and 25 years and presented data for ages at attainment of each stage, age of subject within a stage, and ages at midpoints between attainments of consecutive stages.
Aims of this study
1. To test the accuracy of various age estimation methods using Demirjian’s stages for mandibular seven teeth.
2. To assess the correlation between dental age and chronological age in boys and girls.
Materials and Methods
This cross sectional study sample consisted of 660 (330 boys, 330 girls) randomly selected digital Orthopantomographs (OPG’s) of age ranging from 6 to 16 years (of South Indian descent) divided in to five groups according to age [Table 1]. As the study was retrospective, ethical clearance was not required. All the radiographs were examined by two authors and they assessed the stages of maturation on the basis of calcification of the permanent teeth in mandibular left side from central incisor (I1) to second molar (M2) using Demirjian et al. method. The exclusion criteria were unclear radiographs, presence of any systemic disease, missing teeth, distinct retardation of dental development.
| Chronological Age | Sex | Total | ||||
|---|---|---|---|---|---|---|
| Male | Female | |||||
| Count | % | Count | % | Count | % | |
| 6-7.99 | 14 | 4.2% | 10 | 3.0% | 24 | 3.6% |
| 8-9.99 | 38 | 11.4% | 42 | 12.8% | 80 | 12.1% |
| 10-11.99 | 74 | 22.3% | 78 | 23.8% | 152 | 23.0% |
| 12-13.99 | 96 | 29.5% | 104 | 31.1% | 200 | 30.3% |
| ≥14 | 108 | 32.5% | 96 | 29.3% | 204 | 30.9% |
| Total | 330 | 100.0% | 330 | 100.0% | 660 | 100.0% |
Table 1: Age groups and gender distribution of the panoramic radiographs.
All the 14 methods assessed in this study utilized Demirjian’s stages for analyzing tooth maturation. All of the teeth (from central incisor I1 to second molar M2) of the lower left jaw except third molar were rated on an 8-stage scale ranging from A-H according to Demirjian et al method. [11-13]. Fourteen methods analysed were Demirjian (DM) et al. [2]. Willems I (WI) [3]. Willems II (WII) Chaillet (CH) et al. [5]. Liversidge et al. [10,13]. Nystrom M et al. [11]. Methods L9 (probit mean age entering tooth stages) and L10 (mean age within stage) were Tables 2 and 3, L9a (adapted probit mean age) from Liversidge et al. 2006. Method L10a (adapted probit mean age) was Table 4 form Liversidge 2010. Dental age was also estimated using pooled (P) sex (L9 P, L9a P, L10a P) values from L9, L9a, L10 a. Methods Ny (mean age entering a stage), NyA (age at midpoint between two consecutive stages), NyM (mean age within stage) were Tables 2-5 from Nystrom et al. in 2007.
| Method | I 1 | I2 | C | P1 | P2 | M1 | M2 |
|---|---|---|---|---|---|---|---|
| L10a | -4.79 (2.23)** | -4.07(2.21)** | -1.84(1.73)** | -1.67(1.57)** | -1.00(1.79)** | -4.28(2.26)** | -0.94(1.82)** |
| L9a | -5.04(2.26)** | -4.25(2.2)** | -1.87(1.74)** | -1.76(1.56)** | -1.00(1.64)** | -4.46(2.27)** | -0.99(1.82)** |
| NyM | -4.89(2.24)** | -4.13(2.25)** | -2.02(1.82)** | -2.00(1.60)** | -1.27(1.65)** | -4.43(2.2)** | -1.07(1.7)** |
| L9 | -4.50(2.13)** | -3.79(1.96)** | -1.87(1.58)** | -1.95(1.56)** | -1.08(1.77)** | -3.66(1.8)** | -1.68(1.8)** |
| L10 | -4.69(2.23)** | -3.97(2.25)** | -2.11(1.81)** | -1.74(1.55)** | -1.08(1.65)** | -4.07(2.37)** | -1.07(1.73)** |
| Ny | -4.67(2.15)** | -3.86(2.02)** | -1.94(1.68)** | -1.62(1.7)** | -0.87(1.88)** | -3.62(1.81)** | -1.50(1.93)** |
| NyA | -5.05(2.26)** | -4.39(2.21)** | -2.00(1.76)** | -1.96(1.56)** | -1.17(1.62)** | -4.59(2.26)** | -0.99(1.85)** |
| DM | -0.55(2.25)** | 0.82(1.99)** | -1.38(1.78)** | 0.27(1.87)** | 0.91(1.82)** | 4.42(2.36)** | 0.90(2.02)** |
| CH | -0.59(2.11)** | -0.56(2.00)** | -0.18(1.82)* | -0.42(1.81)** | 0.23(2.01)** | -0.57(2.0)** | -0.54(1.95)** |
| L9aP | -5.06(2.28)** | -4.06(2.26)** | -1.89(1.73)** | -1.78(1.59)** | -1.01(1.65)** | -4.49(2.35)** | -1.04(2.73)** |
| L10aP | -4.76(2.22)** | -4.06(2.2)** | -1.75(1.74)** | -1.65(1.58)** | -0.97(1.65)** | -4.28(2.2)** | -0.91(1.75)** |
| L10P | -4.67(2.22)** | -3.88(2.34)** | -1.86(1.73)** | -1.78(1.57)** | -1.11(1.63)** | -4.16(2.21)** | -1.08(1.73)** |
** P<0.001.
Table 2 : Bias and SD in Years of individual teeth (all stages combined).
| Method | Percentage aged to 0.5 year of actual age | Percentage aged to ≤ 10% of actual age | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Demirjian stages | I 1 | I2 | C | P1 | P2 | M1 | M2 | I 1 | I2 | C | P1 | P2 | M1 | M2 |
| L10a | 1.2% | 3.0% | 15.8% | 12.4% | 17.3% | 1.2% | 21.8% | 2.1% | 8.8% | 33.6% | 31.8% | 42.7% | 3.9% | 50.3% |
| L9a | 0.6% | 2.1% | 13.9% | 12.7% | 17.6% | 1.5% | 20.3% | 2.1% | 5.5% | 33.6% | 31.5% | 43.0% | 2.4% | 46.7% |
| NyM | 1.5% | 3.6% | 14.2% | 11.8% | 17.0% | 1.2% | 22.7% | 2.1% | 7.9% | 32.1% | 25.2% | 40.6% | 2.1% | 46.1% |
| L9 | 0.3% | 3.9% | 8.8% | 11.5% | 16.4% | 3.0% | 12.4% | 1.5% | 7.6% | 24.8% | 26.1% | 43.6% | 5.8% | 38.2% |
| L10 | 1.8% | 3.9% | 13.9% | 12.7% | 17.0% | 1.5% | 21.8% | 2.1% | 10.0% | 27.3% | 30.9% | 44.5% | 6.4% | 45.8% |
| Ny | 0.9% | 3.0% | 6.7% | 13.9% | 17.3% | 3.9% | 15.8% | 1.2% | 6.1% | 23.3% | 31.8% | 50.0% | 7.6% | 42.1% |
| NyA | 0.6% | 1.5% | 14.8% | 11.8% | 16.7% | 0.9% | 20.3% | 1.8% | 3.3% | 30.0% | 27.3% | 41.8% | 1.5% | 47.0% |
| DM | 13.3% | 14.8% | 16.7% | 17.9% | 20.3% | 1.8% | 20.6% | 31.8% | 43.3% | 40.0% | 46.7% | 50.6% | 8.8% | 48.5% |
| CH | 14.5% | 19.1% | 21.2% | 20.0% | 23.6% | 18.8% | 24.5% | 39.1% | 40.9% | 54.8% | 48.2% | 52.7% | 41.5% | 52.7% |
| L9aP | 1.2% | 3.0% | 14.8% | 11.2% | 17.6% | 1.2% | 12.4% | 2.4% | 6.4% | 32.1% | 29.7% | 44.5% | 2.4% | 34.2% |
| L10aP | 1.2% | 3.0% | 15.8% | 12.7% | 20.0% | 1.2% | 19.7% | 2.4% | 7.3% | 33.0% | 33.6% | 45.5% | 3.9% | 49.4% |
| L10P | 1.5% | 0.9% | 14.8% | 12.7% | 14.8% | 1.5% | 21.2% | 2.7% | 8.5% | 32.1% | 26.7% | 43.3% | 5.2% | 46.4% |
Bold indicates best per tooth.
Table 3 : Percentage of individuals aged to 0.5 year and to = 10% of age by individual tooth type.
| Method | Boys | Girls | Total sample |
|---|---|---|---|
| r-value | r-value | r-value | |
| W2 | .751** | .849** | .778** |
| L10a | .727** | .742** | .731** |
| L9a | .698** | .779** | .729** |
| NyM | .711** | .762** | .724** |
| L9 | .740** | .855** | .790** |
| L10 | .719** | .785** | .742** |
| Ny | .751** | .858** | .797** |
| NyA | .739** | .791** | .751** |
| DM | .768** | .878** | .812** |
| W1 | .794** | .880** | .831** |
| CH | .695** | .834** | .756** |
| L9aP | .713** | .781** | .731** |
| L10aP | .724** | .775** | .734** |
| L10P | .724** | .781** | .738** |
** denotes P<0.001.
Table 4: Correlation between DA and CA in boys and girls.
| Method | Age groups | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 6-7.99 | 8-9.99 | 10-11.99 | 12-13.99 | 14-16.99 | ||||||
| Mean | SD | Mean | SD | Mean | SD | Mean | SD | Mean | SD | |
| W2 | 0.80 | 3.02 | -0.80 | 1.15 | -0.16 | 1.88 | -0.43 | 1.61 | -0.74 | 1.61 |
| L10a | -0.08 | 1.63 | -0.91 | 1.02 | -1.41 | 0.91 | -2.71 | 0.67 | -4.58 | 0.74 |
| L9a | -0.40 | 1.65 | -0.99 | 0.92 | -1.57 | 0.97 | -2.88 | 0.74 | -4.71 | 0.72 |
| NyM | 0.01 | 1.67 | -0.94 | 0.79 | -1.58 | 0.85 | -2.93 | 0.65 | -4.82 | 0.79 |
| L9 | -0.42 | 1.95 | -1.66 | 0.94 | -1.66 | 1.17 | -2.63 | 0.82 | -4.06 | 0.86 |
| L10 | 0.08 | 1.57 | -0.81 | 0.79 | -1.40 | 0.92 | -2.71 | 0.61 | -4.60 | 0.73 |
| Ny | -0.77 | 1.98 | -1.65 | 0.96 | -1.73 | 1.32 | -2.50 | 0.93 | -3.86 | 0.83 |
| NyA | -0.28 | 1.61 | -1.09 | 0.81 | -1.63 | 0.88 | -2.91 | 0.66 | -4.77 | 0.75 |
| DM | -0.12 | 1.75 | -0.20 | 1.22 | 0.49 | 1.85 | 0.16 | 1.75 | -0.09 | 1.44 |
| W1 | -0.18 | 1.82 | -0.70 | 1.04 | -0.12 | 1.80 | -0.27 | 1.46 | -0.60 | 1.37 |
| CH | -0.28 | 2.25 | -2.20 | 0.62 | -2.03 | 2.01 | -2.44 | 2.05 | -1.62 | 2.18 |
| L9aP | -0.24 | 1.52 | -1.07 | 1.07 | -1.60 | 0.97 | -2.83 | 0.69 | -4.71 | 0.73 |
| L10aP | -0.35 | 1.74 | -0.81 | 0.93 | -1.34 | 0.94 | -2.63 | 0.60 | -4.56 | 0.73 |
| L10P | -0.25 | 1.60 | -0.77 | 0.87 | -1.38 | 0.90 | -2.69 | 0.59 | -4.64 | 0.71 |
| P value | 0.64 | <0.001 | <0.001 | <0.001 | <0.001 | |||||
Table 5: Bias and Standard deviation by year age cohort.
To assess the reproducibility (inter observer error) and the repeatability (intra-observer error) of this analysis, a subset of 50 OPG’s were randomly chosen and assessed by two examiners after 1 month. A weighted ANOVA was performed on the data of 14 methods using the linear models procedure in order to adapt the scoring systems to present sample using Statistical Package for the Social Sciences computer software (SPSS, version 23.0, SPSS Inc., Chicago, IL, USA). Accuracy refers to how close DA is to CA and reliability is the degree to which measurements and calculations give the same results (Intra and Inter observer agreement). The CA was subtracted from the DA: a positive result indicates an overestimation and a negative result indicates an underestimation of age.
Results
All results were analyzed by two methods, one by combining all developing teeth and all stages for the entire age range and two, by individual tooth type [Tables 2-7]. Relationship between CA and estimated DA was calculated by each method [Table 5] and age groups as well as in total population by analyses of means (standard deviation) and mean obsolute difference (MAD). The differences were considered significant when the p value is less than 0.05.
| Method | Inter-class Correlations | Intra-class correlations | ||
|---|---|---|---|---|
| A1 Vs B1 age | A2 Vs B2 age | A1 Vs A2 age | B1 Vs B2 age | |
| W2 | .938** | .954** | .960** | .954** |
| L10a | .936** | .820** | .815** | .978** |
| L9a | .922** | .980** | .942** | .952** |
| NyM | .913** | .974** | .942** | .943** |
| L9 | .945** | .977** | .975** | .983** |
| L10 | .970** | .980** | .945** | .963** |
| Ny | .969** | .978** | .962** | .971** |
| NyA | .948** | .984** | .978** | .949** |
| DM | .815** | .823** | .890** | .702** |
| W1 | .974** | .883** | .819** | .872** |
| CH | .929** | .871** | .883** | .830** |
| L9aP | .931** | .969** | .965** | .972** |
| L10aP | .962** | .983** | .981** | .973** |
| L10P | .973** | .980** | .979** | .980** |
** denotes P<0.001.
Table 6: Inter and Intra-class correlations.
| Method | N | Bias | SD | P value | Bias rank | Mean obsolute difference (MAD) |
|---|---|---|---|---|---|---|
| W2 | 660 | -0.46 | 1.73 | .000** | 3 | 1.1 |
| L10a | 660 | -2.67 | 1.68 | .000** | 10 | 1.26 |
| L9a | 660 | -2.83 | 1.68 | .000** | 12 | 1.29 |
| NyM | 660 | -2.85 | 1.72 | .000** | 13 | 1.27 |
| L9 | 660 | -2.65 | 1.46 | .000** | 7 | 1.1 |
| L10 | 660 | -2.66 | 1.69 | .000** | 8 | 1.24 |
| Ny | 660 | -2.58 | 1.42 | .000** | 5 | 1.09 |
| NyA | 660 | -2.88 | 1.66 | .000** | 14 | 1.22 |
| DM | 660 | +0.10 | 1.64 | .101 | 1 | 1.0 |
| W1 | 660 | -0.39 | 1.50 | .000** | 2 | 1.06 |
| CH | 660 | -1.98 | 2.02 | .000** | 4 | 1.17 |
| L9aP | 660 | -2.82 | 1.68 | .000** | 11 | 1.28 |
| L10aP | 660 | -2.63 | 1.68 | .000** | 6 | 1.27 |
| L10P | 660 | -2.67 | 1.69 | .000** | 9 | 1.25 |
** P<0.001.
Table 7: Bias and Mean obsolute difference in years of dental age estimation methods.
Comparison between the DA using Willems II method and CA
Mean CA for boys was 12.53 (2.4) y and mean DA was 11.49 (2.71) y. In boys, except in 6-7.99y age group, in all other age groups statistically significant differences were observed and mean DA was underestimated, however underestimation of 1.04 y was noted in whole sample when compared to CA.
In girls, mean CA was 12.38 (2.29) y and mean DA was 12.51 (2.65) y. In all the age groups DA was overestimated except in 8-9.99 y age groups and was significant. In whole sample, DA was overestimated by 0.12 y in girls compared to CA.
Comparison between the DA using L10a method and CA
Mean CA for boys was 12.53 (2.4) y and Mean DA was 9.9 (1.29) y. In boys, except in 6-7.99 y age group, in all other age groups statistically significant differences were observed and mean DA was underestimated, however underestimation of 2.63 (1.71) y was noted in whole sample when compared to CA.
For girls, mean CA was 12.38 (2.29) y and mean DA was 9.67 (1.06) y. In all age groups statistically significant differences were observed and mean DA was underestimated, however underestimation of 2.72 (1.66) y was noted in whole sample when compared to CA.
Comparison between the DA using L9a method and CA
Mean CA for boys was 12.53 (2.4) y and Mean DA was 9.67 (1.34) y. In boys, except in 6-7.99 y age group, in all other age groups statistically significant differences were observed and mean DA was underestimated, however underestimation of 2.86 (1.75) y was noted in whole sample when compared to CA.
For girls, mean CA was 12.38 (2.29) y and mean DA was 9.59 (1.04) y. In all age groups statistically significant differences were observed and mean DA was underestimated, however underestimation of 2.79 (1.61) y was noted in girls in whole sample when compared to CA.
Comparison between the DA using NyM method and CA
Mean CA for boys was 12.53 (2.4) y and Mean DA was 9.8 (1.19) y. In boys, except in 6-7.99 y age group, in all other age groups statistically significant differences were observed and mean DA was underestimated, however underestimation of 2.73 (1.76) y was noted in whole sample when compared to CA.
For girls, mean CA was 12.38 (2.29) y and mean DA was 9.41 (0.96) y. In all age groups statistically significant differences were observed and mean DA was underestimated, however underestimation of 2.97 (1.68) y was noted in girls in whole sample when compared to CA.
Comparison between the DA using L9 method and CA
Mean CA for boys was 12.53 (2.4) y and Mean DA was 9.86 (1.75) y. In boys, except in 6-7.99 y age group, in all other age groups statistically significant differences were observed and mean DA was underestimated, however underestimation of 2.67 (1.61) y was noted in whole sample when compared to CA.
For girls, mean CA was 12.38 (2.29) y and mean DA was 9.76 (1.47) y. In all age groups statistically significant differences were observed and mean DA was underestimated, however underestimation of 2.63 (1.28) y was noted in girls in whole sample when compared to CA.
Comparison between the DA using L10 method and CA
Mean CA for boys was 12.53 (2.4) y and Mean DA was 9.97 (1.19) y. In boys, except in 6-7.99 y age group, in all other age groups statistically significant differences were observed and mean DA was underestimated, however underestimation of 2.56 (1.75) y was noted in whole sample when compared to CA.
For girls, mean CA was 12.38 (2.29) y and mean DA was 9.62 (1.0) y. In all age groups statistically significant differences were observed and mean DA was underestimated, however underestimation of 2.77 (1.62) y was noted in girls in whole sample when compared to CA.
Comparison between the DA using Ny method and CA
Mean CA for boys was 12.53 (2.4) y and Mean DA was 9.8 (1.82) y. In boys, except in 6-7.99 y age group, in all other age groups statistically significant differences were observed and mean DA was underestimated, however underestimation of 2.73 (1.58) y was noted in whole sample when compared to CA.
For girls, mean CA was 12.38 (2.29) y and mean DA was 9.96 (1.64) y. In all age groups statistically significant differences were observed and mean DA was underestimated, however underestimation of 2.42 (1.22) y was noted in girls in whole sample when compared to CA.
Comparison between the DA using NyA method and CA
Mean CA for boys was 12.53 (2.4) y and Mean DA was 9.76 (1.29) y. In boys, except in 6-7.99 y age group, in all other age groups statistically significant differences were observed and mean DA was underestimated, however underestimation of 2.77 (1.68) y was noted in whole sample when compared to CA.
For girls, mean CA was 12.38 (2.29) y and mean DA was 9.4 (0.98) y. In all age groups statistically significant differences were observed and mean DA was underestimated, however underestimation of 2.98 (1.63) y was noted in girls in whole sample when compared to CA.
Comparison between the DA using Demirjian method and CA
Mean CA for boys was 12.53 (2.4) y and Mean DA was 12.31 (2.93) y. Mean DA was underestimated, in all the age groups except in 6-7.99 and 10-11.99 y age groups. However underestimation of 0.22 (1.88) y was noted in whole sample when compared to CA and was significant.
For girls, mean CA was 12.38 (2.29) y and mean DA was 12.82 (2.66) y. In all the age groups mean DA was overestimated except in 6-7.99 and 8-9.99 y age groups and was significant, however overestimation of 0.43 (1.28) y was noted in girls in whole sample when compared to CA.
Comparison between the DA using Willems 1 method and CA
Mean CA for boys was 12.53 (2.4) y and Mean DA was 11.88 (2.64) y. Mean DA was underestimated in all the age groups except in 6-7.99 y age group, however underestimation of 0.65 (1.64) y was noted in whole sample when compared to CA.
For girls, mean CA was 12.38 (2.29) y and mean DA was 12.27 (2.74) y. In all the age groups mean DA was underestimated except in 10-11.99 y age groups and was significant, however underestimation of 0.12 (1.3) y was noted in girls in whole sample when compared to CA.
Comparison between the DA using Chaillet method and CA
Mean CA for boys was 12.53 (2.4) y and Mean DA was 10.15 (2.86) y. Mean DA was underestimated in all the age groups except in 6-7.99 y age group, however underestimation of 2.38 (2.09) y was noted in whole sample when compared to CA.
For girls, mean CA was 12.38 (2.29) y and mean DA was 10.8 (3.29) y. In all the age groups mean DA was underestimated and was significant, however underestimation of 1.58 (1.87) y was noted in girls in whole sample when compared to CA.
Comparison between the DA using L9a Pooled method and CA
Mean CA for boys was 12.53 (2.4) y and Mean DA was 9.48 (1.3) y. In boys, except in 6-7.99 y age group, in all other age groups statistically significant differences were observed and mean DA was underestimated by 3.05 (1.73) y in whole sample when compared to CA.
For girls, mean CA was 12.38 (2.29) y and mean DA was 9.79 (1.08) y. In all age groups statistically significant differences were observed and mean DA was underestimated, however underestimation of 2.59 (1.59) y was noted in girls in whole sample when compared to CA.
Comparison between the DA using L10a Pooled method and CA
Mean CA for boys was 12.53 (2.4) y and Mean DA was 9.68 (1.29) y. In boys, except in 6-7.99 y age group, in all other age groups statistically significant differences were observed and mean DA was underestimated by 2.85 (1.71) y in whole sample when compared to CA.
For girls, mean CA was 12.38 (2.29) y and mean DA was 9.98 (1.04) y. In all age groups statistically significant differences were observed and mean DA was underestimated, however underestimation of 2.41 (1.62) y was noted in girls in whole sample when compared to CA.
Comparison between the DA using L10 Pooled method and CA
Mean CA for boys was 12.53 (2.4) y and Mean DA was 9.68 (1.21) y. In boys, except in 6-7.99 y age group, in all other age groups statistically significant differences were observed and mean DA was underestimated by 2.84 (1.73) y in whole sample when compared to CA.
For girls, mean CA was 12.38 (2.29) y and mean DA was 9.92 (1.00) y. In all age groups statistically significant differences were observed and mean DA was underestimated, however underestimation of 2.47 (1.63) y was noted in girls in whole sample when compared to CA.
Correlation between DA assessed by 14 methods using Demirjian stages and CA
Reliability of all the fourteen age estimation methods was verified by testing intra-and inter-observer agreement and was found to be highly reliable [Table 6]. Pearson correlation showed strong association between CA and DA [Table 4].
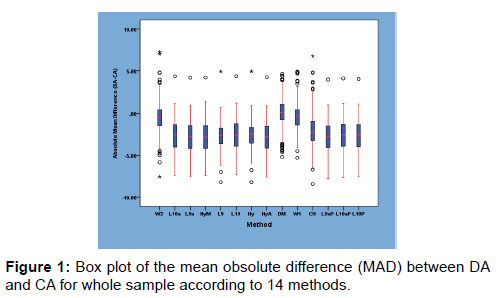
Our results showed that only Demirjian method estimated age with bias not significant to zero. Other methods which showed little bias were Willems I, Willems II and Chaillet methods. All the methods underestimated age except Demirjian method. The standard deviation for all the methods was between 1.42 and 2.02 years. The method with the smallest mean obsolute difference was Original Demirjian method followed by WI method. The mean obsolute difference was similar for several other methods, WII and L9 (MAD-1.1), L10a, NyM, L9aP, L10aP (MAD-1.27) [Figure 1].
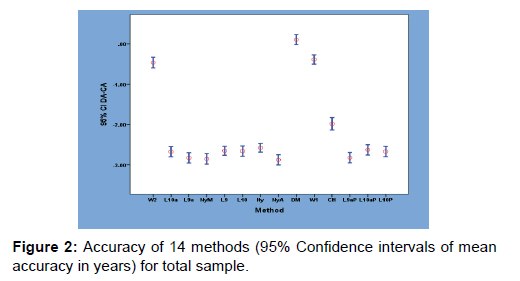
The methods with the highest percentage of individual aged to within six months of real age and the highest proportion aged to 10% or less of age was Demirjian, WI, W II methods. [Figure 2] Results of bias and measures of accuracy for individual teeth (all stages combined) were shown in Tables 7 and 8. All the methods performed well with seven teeth estimating bias not significant to zero. The percentage of individuals aged to 0.5 years to known age for individual teeth varied from 24.5% (CH second molar) to 0.3% (L9 central incisor). The percentage of individuals aged to within 10% or less of age for individual teeth was highest at 54.8% (Chaillet canine), 50.3% (L10a second molar), 50% (Ny second premolar), 48.5% (Demirjian second molar). The worst tooth was L9 central incisor (1.5%).
| Method | N | % <0.5 years | <10% of age |
|---|---|---|---|
| W2 | 660 | 28.2% | 56.4% |
| L10a | 660 | 6.4% | 16.1% |
| L9a | 660 | 5.5% | 13.3% |
| NyM | 660 | 5.5% | 13.3% |
| L9 | 660 | 4.8% | 12.7% |
| L10 | 660 | 7.3% | 17.3% |
| Ny | 660 | 6.4% | 11.2% |
| NyA | 660 | 5.5% | 12.1% |
| DM | 660 | 30.0% | 61.5% |
| W1 | 660 | 30.3% | 60.0% |
| CH | 660 | 9.4% | 22.4% |
| L9aP | 660 | 4.8% | 12.1% |
| L10aP | 660 | 4.2% | 18.5% |
| L10P | 660 | 4.8% | 17.9% |
Table 8: Percentage of individuals aged to within 0.5 years and ≤10% of age.
Discussion
Dental age is not the same for all children of a specific known age. Developing tooth with crown and root stages is usually used to assess maturity or estimate age for an individual child. Studies testing the accuracy of various dental age estimation methods may get affected by different sample sizes, nonuniform age distribution and statistical methods applied. In this study the effectiveness of 14 methods was compared in terms of mean obsolute accuracy between the estimated and actual age and the number of age estimates that were either <±1 year ( up to 2 years considered as accurate) or >±2 year (considered as inaccurate) from actual age. [11]. In the present study, all the assessed 14 methods were found to be accurate as the mean obsolute difference values were less than 2 years. The method with the smallest mean obsolute difference was Demirjian and Willems I methods (more accurate) and with highest mean obsolute difference was L9a method (least accurate).
Numerous studies, where Demirjian method alone was applied to assess age, showed consistent overestimation [6,12-20] and was found to be more accurate , in accordance with this study. [21]. This overestimation may be explained by factors such as the biological variations in children, positive trend in growth, and development, differences in population, sample size, age distribution and statistical approach. [22,23].
In the present study, Willems I method underestimated age [18,23-26]. and was found to be accurate method for age estimation as noted in previous studies. [15,19,23,27-29]. Chaillet method underestimated age as noted in previous study [19,23,28,30] and did not yield expected results compared to other maturity scales even though the method was not dependent on ethnicity, in contrast to previous study. [19].
Liversidge et al. [28]. studied data from Maber et al. [23]. and showed that method which performed best was WI method with mean obsolute difference of 0.66 years which was slightly less compared to our study. They showed that methods that average ages for individual teeth improved if schedules for ‘mean age entering a stage’ were adjusted for prediction and methods that directly calculate ‘mean age within stage’ can be improved by drawing from a uniform age distribution and also stated that no major differences in tooth formation exist between children in selected sample, similar results were observed in present study.
Liversidge HM. [31]. stated that Demirjian’s method remains a valid scale to assess maturity of the individual child and is probably applicable to any region. Only a few studies [32]. compare dental maturity of individual teeth in populations using average age entering tooth stages and found similarities between ethnic and regional groups. In Liversidge et al [10]. study, mean age at entry for individual tooth stages was compared in the groups of children belonging to eight countries and a small group from one country (Korea) showed a wide age range of individuals within each tooth stage with many similarities in average age at entry.
Liversidge [33]. reexamined the data from previous analyses [23,28,34]. that provide a point estimate using developing second molar and stated that adapted maturity data L9a (probit mean age adapted for age prediction) performed best for second molar among Demirjian tooth stages and was suitable to estimate age from 3-14 years of age. This study also suggested that pooled sex reference data were as good as sex-specific methods to estimate dental age from developing teeth and population specific reference data do not improve estimates of dental age. Our results cannot be compared with this study as the methods of assessment applied were different.
Liversidge [3]. explained that during the process of assessing maturity or age of a child, the individual is compared to reference data, where differences between groups are important. Small differences in the mean age of individual tooth stages at the group level have little influence on the estimated age for an individual and population specific standards may be not necessary for age estimation.
A uniform age distribution with similar numbers for each year of age is required in both reference and target samples to obtain desired results. This study was cross-sectional and retrospective, where radiographs relating to younger age groups were limited because it is uncommon for younger children to go for panoramic radiographs with normally developing dentition.
Conclusion
This study showed that Original Demirjian method was found to be more accurate followed by Willems I and Willems II methods for age estimation. All the methods assessed were found to be reliable for age estimation in South Indians. The present study also showed that methods that average ages for individual teeth improve if ‘mean age entering a stage’ values were adjusted for age prediction and methods that calculate ‘mean age within stage’ can be improved by applying the methods on uniform age distribution sample.
Conflict of Interest
All authors disclose that there was no conflict of interest.
REFERENCES
- Cunha E, Baccino E, Martrille L, Ramsthaler F, Prieto J, Schullar Y. The Problem of aging human remains and living individuals:a review. Forensic Sci Int 2009; 15:193: 1-13.
- Smith BH. 1991. Standards of human tooth formation and dental age assessment. In: Kelley M, Larsen CS, editors. Advances in dental anthropology. New York: Alan R. Liss. P 143-68.
- Liversidge HM. 2010. Demirjian stage tooth formation results from a large group of children. Dent Anthropol 23:16-24.
- Demirjian A, Goldstein H, Tanner JM. A new system of dental age assessment. Hum Biol 1973;45: 211-227
- Jin Yan, Xintian Lou, Liming Xie, Dedong Yu, Guofang Shen, Wang Y. Assessment of Dental age of children aged 3.5 to 16.9 years using Demirjian’s method: A meta-analysis based on 26 studies. PLOS ONE 2013:8: 12:e84672.
- Willems G, Van Olmen A, Spiessens B, Carels C. Dental Age Estimation in Belgian Children: Demirjian’s Technique Revisited. J Forensic Sci 2001; 46: 893-895.
- Chaillet N, Nystrom M, Demirjian A. 2005. Comparison of dental maturity in children of different ethnic origins: International maturity curves for clinicians. J Forensic Sci 50: 1164-1174.
- Nystrom M, Ranta HM, Peltola S, Kataja JM. 2007. Timing of developmental stages in permanent mandibular teeth of Finns from birth to age 25. Acta Odont Scand 65: 36-43.
- Willems G, Thevissen PW, Belmans A, Liversidge HM. 2010. Willems II. Non-gender-specific dental maturity scores. Forensic Sci Int 2010 (201) 84-85.
- Liversidge HM, Chaillet N, Mo¨rnstad H, Nystrom M, Rowlings K, Taylor J, Willems G. 2006. Timing of Demirjian’s tooth formation stages. Ann Hum Biol 33: 454-470.
- Ferrante L, Cameriere R. Statisticalmethods to assess the reliability of measurements in the procedures for forensic age estimation. Int J Leg Med 2009; 123: 4:277-283.
- Eid RM, Simi R, Friggi MN, Fisberg M. 2002. Assessment of dental maturity of Brazilian children aged 6 to 14 years using Demirjian’s method. Inter J Paed Dent 12: 423-428.
- Hegde RJ, Sood PB. Dental maturity as an indicator of chronological age: radiographic evaluation of dental age in 6 to 13 years children of Belgaum using Demirjian methods. J Indian Soc Pedod Prev Dent. 2002; 20:132-138.
- Koshy S and Tandon S. Dental age assessment: The applicability of Demirjian’s method in South Indian children. J Forensic Sci 1998; 94:73-85.
- Mani SA, Naing L, John J, Samsudin AR. Comparison of two methods of dental age estimation in 7-15-year-old Malays. Int J Paediatr Dent. 2008; 18:380-388.
- Al-Emran S. Dental age assessment of 8.5 to 17 year-old Saudi children using Demirjian’s method. J Contemp Dent Pract. 2008; 9: 64-71.
- Tunc ES, Koyuturk AE. Dental age assessment using Demirjian’s method on northern Turkish children. Forensic Sci Int. 2008; 175: 23-26.
- Rezwana Begum MD, Sanghvi P, Kiran kumar P,Srinivasaraju D, Srinivas J, Iftekhar Rasool SM. Accuracy of four dental age estimation methods in Southern Indian children. J Clinical and Diagnostic Research 2015; 9:1:HC01-HC08.
- Urzel V, Bruzek J. Dental age assessment in children: A comparison of four methods in a recent French population. J Forensic Sci. 2013; 58: 1341-1347.
- Cukovic Bagic I, Sever N,Brkic H, Kern J. Dental age estimation in children using orthopantomograms. Acta Stomatol Croat 2008; 42:1: 11-18.
- Pinchi V, Norelli GA, Pradella F, Vitale G, Rugo D, Nieri M. Comparison of the applicability of four odontological methods for age estimation of the 14 years legal threshold in a sample of Italian adolescents. J Forensic Odontostomatol. 2012; 30:17-25.
- Liversidge HM, Speechly T, Hector MP. Dental maturation in British children: are Demirjian’s standards applicable? Int J Paediatr Dent 1999; 9:263-9.
- Maber M,Liversidgr HM,Hector MP. Accuracy of age estimation of radiographic methods using developing teeth. Forensic Sci Int 2006; 159S:S68-73.
- Rezwana Begum MD, P. V. Krishnamraju, P. S. Prasanth, Sanghvi P, M. Asha Lata Reddy, S. Jyotsna. Dental age estimation using Willems method: A digital orthopantomographic study. Contemporary Clinical Dentistry 2014; 5: 3; 371-376.
- Liversidge HM. Dental age revisited. In: Irish JD, Nelson GC, editors. Technique and Application in Dental Anthropology. Cambridge: Cambridge University Press; 2008. p. 234-52.
- Cameriere R, Ferrante L, Liversidge HM, Prieto JL, Brkic H. Accuracy of age estimation in children using radiograph of developing teeth. Forensic Sci Int 2008; 176:173-177.
- Rai B, Anand SC. 2006. Tooth developments: an accuracy of age estimation of radiographic methods. World J Med Sci 1:130-132.
- Liversidge HM, Smith BH, Maber M. 2010. Bias and accuracy of age estimation using developing teeth in 946 children. Am J Phys Anthropol 143: 545-554.
- Nik-Hussein NN,Kee KM, Gan P. Validity of Demirjian and Willems methods for dental age estimation for Malysian children aged 5-15 years old. Forensic Sci Int 2011; 204-208.
- Galic´ I, Vodanovic´ M, Cameriere R, Nakasˇ E, Galic´ E, Selimovic´ E, Brkic´ H. 2010. Accuracy of Cameriere, Haavikko, and Willems radiographic methods on age estimation on Bosnian-Herzegovian children age groups 6-13. Int J Legal Med 125: 315-321.
- Liversidge HM. Interpreting group differences using Demirjian’s dental maturity method. Forensic Sci Int 2010; 201: 95-101.
- Liversidge HM. 2011. Similarity in dental maturation in two ethnic groups of London children. Ann Hum Biol 38: 702-715.
- Liversidge HM. Controversies in age estimation from developing teeth. Annals of Human Biology 2015; 42: 397-406.
- AlQahtani SJ, Hector MP, Liversidge HM. Accuracy of dental age estimation charts Schour and Massler, Ubelaker and the London atlas. Am J Phys Anthropol 2014:154: 70-78.



 The Annals of Medical and Health Sciences Research is a monthly multidisciplinary medical journal.
The Annals of Medical and Health Sciences Research is a monthly multidisciplinary medical journal.